Question

What is the inverse of the function below?

Answer 1

`f(x) = \ln(10x)\\ \\ f^(-1)\Big(f(x)\Big) =x \\ \\ f^(-1)\Big(\ln(10x)\Big) = x\\ \\ \ln(10x) = t \Rightarrow 10x = e^t \Rightarrow x = (e^t)/(10) \\ \\ \Rightarrow f^(-1)(t) = (e^t)/(10) \Rightarrow \boxed{f^(-1)(x) = (e^x)/(10)}`

Answer 2

Hello!

The answer is:

The correct option is:

c)
`f^(-1)(x)=(e^(x))/(10)`

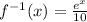
Why?

Inversing a function means switching the range and domain of the function. To inverse a function we need to rewrite the variable (x) with the function (f(x) or y), and rewrite the function (f(x) or y) with the variable (x), and then, isolate "y" or "f(x)".

Also, we need to remember how to isolate the variable from a logarithmic function.

`ln(x)=a\\\\e^(a)=e^(ln(x))\\\\e^(a)=x`

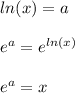
So, we are given the function:

`f(x)=ln(10x)`

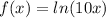
Which it's equal to write:

`y=ln(10x)`

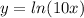
Then, inversing the function we have:

`y=ln(10x)`

`x=ln(10y)`

`x=ln(10y)\\\\e^(x)=e^(ln(10y)) \\e^(x)=10y\\\\y=(e^(x))/(10)`

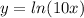
Hence, we have that the correct answer is the option:

c)
`f^(-1)(x)=(e^(x))/(10)`

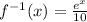
Have a nice day!