Question

Danny is a drummer who purchases his drumsticks online. When practicing with the newest pair, he notices they feel heavier than usual. When he weighs one of the sticks, he finds that it is 2.44 oz. The manufacturer's website states that the average weight of each stick is 2.00 oz with a standard deviation of 0.19 oz. Assume that the weight of the drumsticks is normally distributed. What is the probability of the sticks weight being 2.44 oz or greater?

Answer 1

Probability of the sticks weight being 2.44 oz or greater is 0.01017 .

Explanation:

We are given that the manufacturer's website states that the average weight of each stick is 2.00 oz with a standard deviation of 0.19 oz.

Also, it is given that the weight of the drumsticks is normally distributed.

Let X = weight of the drumsticks, so X ~ N(
`\mu = 2,\sigma^(2) = 0.19^(2)`)

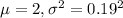The standard normal z distribution is given by;

Z =
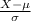`(X-\mu)/(\sigma)` ~ N(0,1)

Now, probability of the sticks weight being 2.44 oz or greater = P(X >= 2.44)

P(X >= 2.44) = P(
`(X-\mu)/(\sigma)` >=
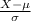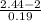`(2.44-2)/(0.19)` ) = P(Z >= 2.32) = 1 - P(Z < 2.32)

= 1 - 0.98983 = 0.01017

Therefore, the probability of the sticks weight being 2.44 oz or greater is 0.01017 .