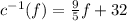For this case we have the following function:
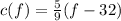
We must find the inverse function. For this we follow the steps below:
Replace c (f) with y:
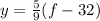
We exchange variables:
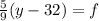 f = \frac {5} {9} (y-32)
f = \frac {5} {9} (y-32)
We solve for "y":
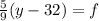
We multiply by
 on both sides of the equation:
on both sides of the equation:
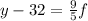
We add 32 to both sides of the equation:

We change y by
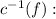
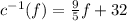
Answer: