Question

Help needed asap 20 points if answered right

Answer 1

1. No real roots

2.
`( 7\pm \: √(33) )/( - 4)`

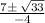
3. The discriminant is negative.

Step-by-step explanation

1. The given equation is

`- 2 {x}^(2) - 9x - 5 = 0`

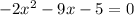
We have a=-2,b=-9 and c=-5.

The discriminant is given by:

`D= {b}^(2) - 4ac`

`D= {( - 9)}^(2) - 4( - 2)( - 5)`

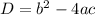
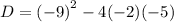
This simplifies to:

`D= 36 - 40 = - 4`

Since the discriminant is less than zero, the quadratic equation has no real roots.

2. The given equation is:

`- 2 {x}^(2) - 7x - 2= 0`

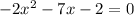
We have a =-2, b=-7 and c=-2.

The roots of this equation are given by;

`x = \frac{ - b \pm \: \sqrt{ {b}^(2) - 4ac } }{2a}`

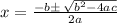
We plug in the values to get;

`x = \frac{ - - 7\pm \: \sqrt{ {( - 7)}^(2) - 4( - 2)( - 2) } }{2( - 2)}`

`x = ( 7\pm \: √(33) )/( - 4)`

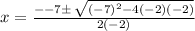
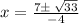
3. The given graph is hanging downwards. This means that it doesn't have x-intercepts.

Therefore the roots are complex or imaginary.

This implies that, the discriminant of the corresponding equation is negative.