Answer:
x = 4
Explanation:
Given a secant and a tangent drawn from an external point to the circle, then
The square of the measure of the tangent is equal to the product of the external part and the entire secant, that is
x(x + 12) = 8²
x² + 12x = 64 ( subtract 64 from both sides )
x² + 12x - 64 = 0 ← in standard form
with a = 1, b = 12 and c = - 64
Using the quadratic formula to solve for x
x = ( - 12 ±
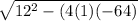 ) / 2
) / 2
= ( - 12 ±
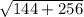 ) / 2
) / 2
= ( - 12 ±
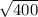 ) / 2
) / 2
x =
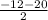 or x =
or x =
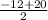
x = - 16 or x = 4
However x > 0 ⇒ x = 4