Question

PLEASE HELP ME NOW URGENT

Answer 1

3±√21. The equation
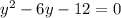`y^(2)-6y-12=0` has two possible solutions 3+√21 y 3-√21.

If we have a general quadratic equation
`ay^(2) +by+c=0` we can solves the equation by completing the square. First, we divide the quadratic equation by a, we obtain
`y^(2) +(b)/(a) y+(c)/(a) =0`.

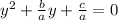For this problem, we have
`y^(2)-6y-12=0`

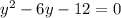
We can skipped division in this example since the coefficient of
`x^(2)` is 1.

Move the term c to the right side of the equation

`y^(2)-6y=12`

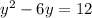
Completing the square on the left side of the equation and balance this by adding the same number to the right side of the equation, with b = -6.

`((b)/(2))^(2) =((-6)/(2))^(2)=(-3)^(2) =9`

`y^(2)-6y+9=12+9`

`(y-3)^(2)=21`

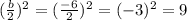
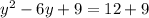
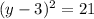
Take the square root on both sides of the equation:

y - 3 = ±√21

Add 3 from both sides:

y = 3 ± √21

Answer 2

`y = 3 \pm √(21)`

Step-by-step explanation

The quadratic equation is:

`{y}^(2) - 6y - 12 = 0`

Group variable terms:

`{y}^(2) - 6y = 12`

Add the square of half, the coefficient of y to both sides.

`{y}^(2) - 6y + ( - 3) ^(2) = 12 + ( - 3) ^(2)`

`{y}^(2) - 6y + 9= 12 + 9`

The LHS us now a perfect square trinomial:

`{(y - 3)}^(2)= 21`

Take square root:

`y - 3 = \pm √(21)`

`y = 3 \pm √(21)`

The first choice is correct.