The value of ∛x^10, when x = -2, can be written in simplest form as a∛b, where a = _ and b = _.

Question

asked Feb 27, 2020 60.0k views

2 Answers

Nixmind · Answer 1 · 2020-03-02T09:55:37+0000

Answer:

a = -8

b = -2

Explanation:

We have been given the following radical expression;

$\sqrt[3]{x^(10) }$

The radical can be expressed using the law of exponents;

$\sqrt[n]{x}=x^{(1)/(n) }$

The radical can thus be re-written as;

$\sqrt[3]{x^(10) }=(x^(10))^{(1)/(3) }$

Using the law of exponents;

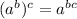
(a^(b))^(c)=a^(bc)

The last expression becomes;

$(x^(10))^{(1)/(3) }=x^{(10)/(3) }=x^(3)*x^{(1)/(3) }\\\\=x^(3)\sqrt[3]{x}$

substituting x with -2 yields;

$-2^(3)\sqrt[3]{-2}=-8\sqrt[3]{-2}$