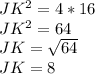Question

Given: JK tangent, KH=16, HE=12 Find: JK.

Answer 1

Both intersecting point K, JK is a tangent and KH is a secant. You can use the intersecting secant-tangent Theorem:

JK^2=KH*EK

First you can do

KH=EK+EH

KE=4

Then you can substitute.

JK^2=64

JK=8

Answer 2

Answer:
`JK=8`

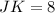
Explanation:

You can observe in the figure that JK is a tangent and KH is a secant and both intersect at the point K. Then, according to the Intersecting secant-tangent Theorem:

`JK^2=KE*KH`

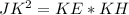
You know that:

`KH=KE+HE`

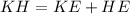
Then KE is:

`KE=KH-HE`

`KE=16-12`

`KE=4`

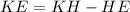
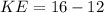
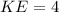
Now you can substitute the value of KE and the value of KH into
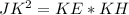`JK^2=KE*KH` and solve for JK. Then the result is:

`JK^2=4*16\\JK^2=64\\JK=√(64)\\JK=8`