Answer:
25.6 units
Explanation:
From the figure we can infer that our triangle has vertices A = (-5, 4), B = (1, 4), and C = (3, -4).
First thing we are doing is find the lengths of AB, BC, and AC using the distance formula:
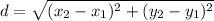
where
 are the coordinates of the first point
are the coordinates of the first point
 are the coordinates of the second point
are the coordinates of the second point
- For AB:
![d=\sqrt{[1-(-5)]^(2)+(4-4)^2}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/dllt5zlmj8h409iuhsy4npfipkrgm1m5ix.png)
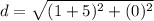
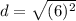
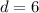
- For BC:

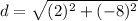
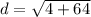
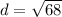

- For AC:
![d=\sqrt{[3-(-5)]^(2) +(-4-4)^(2)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kqgnoi3u9856as4nrju2n4hn1e5l5zg6yb.png)
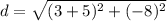
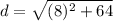
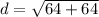
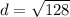
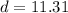
Next, now that we have our lengths, we can add them to find the perimeter of our triangle:
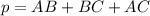
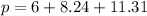
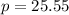

We can conclude that the perimeter of the triangle shown in the figure is 25.6 units.