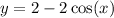Find the particular solution to y'=2sin(x) given the general solution is y=C-2cos(x) and the initial condition y(pi/3)=1 -2cos(x) 3-2cos(x) 2-3cos(x) -1-2cos(x)

Question

asked Mar 27, 2020 147k views

1 Answer

Droidbot · Answer 1 · 2020-04-01T16:18:50+0000

ANSWER

The particular solution is:

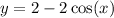
$y=2-2 \cos(x)$

Step-by-step explanation

The given Ordinary Differential Equation is

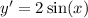
$y'=2 \sin(x)$

The general solution to this Differential equation is:

$y=C-2 \cos(x)$

To find the particular solution, we need to apply the initial conditions (ICs)

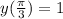
$y( (\pi)/(3) ) = 1$

This implies that;

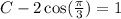
$C-2 \cos( (\pi)/(3) ) = 1$

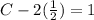
C-2( (1)/(2) )= 1

C-1= 1

C= 1 + 1 = 2

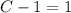
Hence the particular solution is

$y=2-2 \cos(x)$