Question

The function f(x) = x^2 +8x+10 is equivalent to the function f(x)=(x-h)^2+k. What is the value of h and k . At what value of x is the minimum value of the function

Answer 1

`h = - 4,k = - 6`

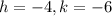
Minimum value: y=-6

Occurs at: x=-4

Step-by-step explanation

Given

`f(x) = {x}^(2) + 8x + 10`

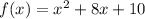
We need to write the equivalent of this function in vertex form:

`f(x) = ({x - h)}^(2) + k`

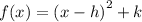
where (h,k) is the vertex.

We must complete the square to get the function to this form.

We add and subtract the square of half the coefficient of x.

`f(x) = {x}^(2) + 8x +( (8)/(2)) ^(2) - ( (8)/(2)) ^(2) + 10`

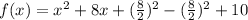
This gives us;

`f(x) = {x}^(2) + 8x +16- 16 + 10`

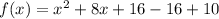
The first three terms form a perfect square quadratic trinomial.

`f(x) =( x + 4) ^(2) - 6`

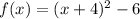
or

`f(x) =( x - - 4) ^(2) - 6`

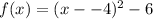
Therefore we compare to

`f(x) = ({x - h)}^(2) + k`

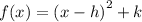
h=-4 and k=-6

The minimum value of the function is

`y = - 6`

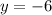
and this occurs at;

`x = - 4`