A cylinder has a radius of 10 cm and a height of 9 cm. A cone has a radius of 10 cm and a height of 9 cm. Show that the volume of a cylinder is three times the volume of the con…

Question

asked Sep 14, 2020 2.2k views

1 Answer

Michal Gasek · Answer 1 · 2020-09-19T21:18:01+0000

Explanation:

We start with the formulas for the volumes of a cylinder and a cone.

Cylinder:

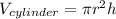
$V_(cylinder) = \pi r^2 h$

Cone:

$V_(cone) = (1)/(3) \pi r^2 h$

Now we calculate the two volumes.

Cylinder:

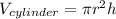
$V_(cylinder) = \pi r^2 h$

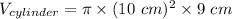
$V_(cylinder) = \pi * (10~cm)^2 * 9~cm$

$V_(cylinder) = \pi * 100~cm^2 * 9~cm$

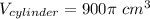
$V_(cylinder) = 900 \pi~cm^3$

Cone:

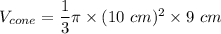
$V_(cone) = (1)/(3) \pi * (10~cm)^2 * 9~cm$

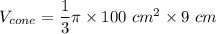
$V_(cone) = (1)/(3) \pi * 100~cm^2 * 9~cm$

$V_(cone) = 300 \pi~cm^3$

The volume of the cylinder is 900pi cm^3, and the volume of the cone is 300pi cm^3.

Now we divide the volume of the cylinder by the volume of the cone.

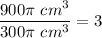
$(900 \pi~cm^3)/(300 \pi~cm^3) = 3$

Dividing the volume of the cylinder by the volume of the cone gives us 3, showing that the volume of the cylinder is 3 times the volume of the cone.