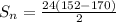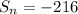Answer:
Sn = -216
Explanation:
We are given the following sequence and we are to find the sum of the given sequence if there are 24 terms in it:
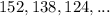
We know that the formula of sum for an arithmetic sequence is given by:
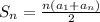
where
 is the first term (124)and
is the first term (124)and
 is the last term
is the last term
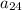 .
.
To find
 , we will use the following formual:
, we will use the following formual:
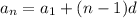
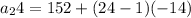
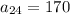
Substituting the given values in the above formula to get the sum: