Question

Use the limit theorem and the properties of limits to find the limit.

Answer 1

Hello!

The answer is:
`d.(√(3) )/(4)`

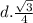
Why?

Since the degree of both numerator and denominator are the same, the result will be a number different of zero, so the first given option (a) it's incorrect.

We need to "break" the indeterminate form of the limit in order to find the correct answer.

To solve this limit, we must divide each term by the largest degree term, for this case is "x" since the numerator is inside of a square root.

So, doing it we can solve the limit:

`\lim_(x \to \infty)\frac{\sqrt{(3x^(2) )/(x^(2) )+(2)/(x^(2))}}{(4x)/(x)+(1)/(x)}\\\\ \lim_(x \to \infty) \frac{\sqrt{3+(2)/(x^(2))}}{4+(1)/(x)}`

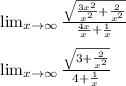
Then, before evaluating the limit, we must remember that any number divided by infinity will give as result zero (0), so:

`\lim_(x \to \infty) \frac{\sqrt{3+(2)/((infinity)^(2))}}{4+(1)/(infinity)}\\\\\lim_(x \to \infty) (√(3+0))/(4+0)=(√(3) )/(4)`

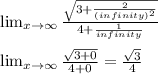
So, the correct option is:
`d.(√(3) )/(4)`

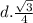
Have a nice day!

Answer 2

The answer is √3/4 ⇒ answer (d)

Explanation:

∵
`\lim_(n \to \infty) \frac{\sqrt{3x^(2)+2} }{4x+1}`

* By using the limit theorem: divide up and down by x

∵ x = √x²

∴
`\sqrt{(3x^(2) )/(x^(2))+(2)/(x^(2))` =

`\sqrt{3+(2)/(x^(2))` ⇒ numerator

∵
`(4x)/(x)+(1)/(x)=4+(1)/(x)` ⇒ denominator

∵ x →∞ ⇒ ∴ 2/x² = 2/∞ = 0 and 1/x = 1/∞ = 0

∴
`\lim_(x \to \infty)\frac{\sqrt{3+(2)/(x^(2))}}{4+(1)/(x)}=(√(3))/(4)`

∴ The answer is √3/4 ⇒ (d)