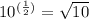Write an equivalent exponential equation for: log_(10) √(10) = (1)/(2)

Question

Write an equivalent exponential equation for:


`log_(10) √(10) = (1)/(2)`

Answer 1

First you put the base which’s ten and put the exponent (half) you put the equal sign and the number beside the log will be the answer

So it will be log the square root of ten to the base ten equals half
(log form )

Ten to the power of half equals the square root of ten

Answer 2

Answer:
`10^{((1)/(2))}=√(10)`

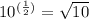
Explanation:

By definition you have that you can write:

`log_b(a)=c`

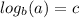
as following:

`b^c=a`

Therefore, keeping the information above on mind, you can write the following equivalent exponential equation for the exppresion given in the problem (
`log_(10)(√(10))=(1)/(2)`):

`10^{((1)/(2))}=√(10)`

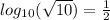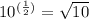
Thenrefore, the answer is:
`10^{((1)/(2))}=√(10)`