In parallelogram ABCD point K belongs to diagonal BD and divides BD so that BK:DK=1:4. If ray AK meets BC at point E, what is the ratio of BE:EC?

Question

asked Oct 24, 2020 135k views

1 Answer

Xurca · Answer 1 · 2020-10-27T23:56:13+0000

Answer:

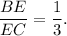
(BE)/(EC)=(1)/(3).

Explanation:

Consider triangles BKE and DKA. In this triangles:

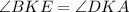$\angle BKE=\angle DKA$ as vertical angles;
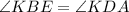$\angle KBE=\angle KDA$ as alternate interior angles (lines BC and AD are parallel and BC is a transversal);
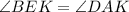$\angle BEK=\angle DAK$ as alternate interior angles (lines BC and AD are parallel and BE is a transversal).

Thus triangles BKE and DKA are similar by AA theorem. Similar triangles have proportional sides lengths:

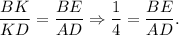
$(BK)/(KD)=(BE)/(AD)\Rightarrow (1)/(4)=(BE)/(AD).$

Thus,
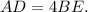
AD=4BE.

Since AD=BC and BC=BE+CE, we have that 4BE=BE+EC, EC=3BE. Hence, the ratio BE to EC is

(BE)/(EC)=(BE)/(3BE)=(1)/(3).