Question

Lin and Tyler are drawing circles. Tyler’s circle has twice the diameter of Lin’s circle. Tyler thinks that his circle will have twice the area of Lin’s circle as well. Do you agree with Tyler?

Answer 1

The answer would be No

Please thank

Answer 2

No, tyler is wrong, his circle´s area has four times the Lin’s circle area.

Explanation:

Hello

Let's remember this about a circle

the area is given by:

`A=\pi r^(2)`

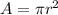
where r is the radius

and the diameter

`D=2r\\isolating \ x\\r=(D)/(2)\\`

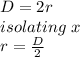
Step 1

according to the question Tyler’s circle has twice the diameter of Lin’s circle,in other terms

Let

`Tylers \ diameter\ (D_(1))  =2\ times\ Lins\ circle(D_(2))\\\\`

`D_(1)=2D_(2)`

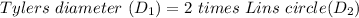
Step 2

find the areas

Area of Tyler’s circle

`A_(1)=\pi  *r_(1) ^(2)`

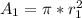
replacing

let r_{1}= Tyler’s circle radius

`r_(1)=(D_(1) )/(2)  \\A_(1)=\pi  *r_(1) ^(2)\\A_(1)=\pi  *((D_(1) )/(2))^(2)\\A_(1)=\pi *(D_(1)^(2) )/(4)`

`let\ r_(2)= Lin\ circle\ radiusr_(2)=(D_(2) )/(2)  \\A_(2)=\pi  *r_(2) ^(2)\\A_(2)=\pi  *((D_(2) )/(2) )^(2)\\A_(2)=\pi *(D_(2)^(2) )/(4)\\\\`

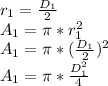
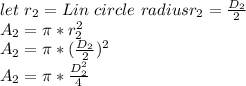
Now, from

`D_(1)=2D_(2)\\so\\\D_(2)=(D_(1) )/(2)  \\`

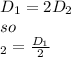
replacing

`A_(2)=\pi *(D_(2)^(2) )/(4)\\A_(2)=\pi *(((D_(1) )/(2)) ^(2) )/(4)\\\\\\`

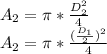
step 3

compare the areas

`A_(1)=\pi *(D_(1)^(2) )/(4)\  and\ A_(2)= \pi *(D_(1)^(2))/(16)\\(A_(1))/(A_(2)) =(\pi *(D_(1)^(2) )/(4))/( \pi *(D_(1)^(2))/(16))\\(A_(1))/(A_(2)) =4\\hence\\A_(1)=4 A_(2)`

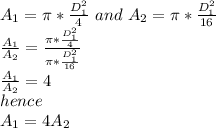
this means that tyler is wrong, his circle´s area has four times the Lin’s circle area.

Have a great day