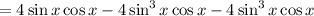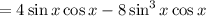Question

How can you prove that
sin4x= 4 cos x sin x - 8 cos x sin(third power)x

Answer 1

If you have some knowledge of complex numbers: This follows pretty much immediately from Euler's formula and DeMoivre's theorem,

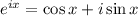`e^(ix)=\cos x+i\sin x` (Euler)

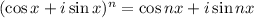`(\cos x+i\sin x)^n=\cos nx+i\sin nx` (DeMoivre)

so that
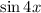`\sin 4x` is the imaginary part of the expanded left hand side.

If that's unfamiliar to you, you can make use of several identities to expand
`\sin4x`:

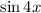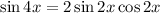`\sin4x=2\sin2x\cos2x` (double angle sine)

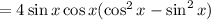`=4\sin x\cos x(\cos^2x-\sin^2x)` (double angle sine and cosine)

`=4\sin x\cos^3x-4\sin^3x\cos x`

`=4\sin x\cos x\cos^2x-4\sin^3x\cos x`

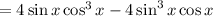
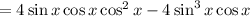
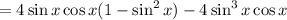`=4\sin x\cos x(1-\sin^2x)-4\sin^3x\cos x` (Pythagorean)

`=4\sin x\cos x-4\sin^3x\cos x-4\sin^3x\cos x`

`=4\sin x\cos x-8\sin^3x\cos x`