Answer:
1+i
Explanation:
To find the 8th roots of unity, you have to find the trigonometric form of unity.
1. Since
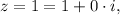 then
then
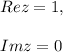
and
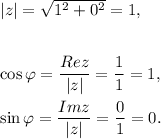
This gives you
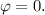
Thus,
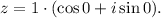
2. The 8th roots can be calculated using following formula:
![\sqrt[8]{z}=\{\sqrt[8]z (\cos(\varphi+2\pi k)/(8)+i\sin (\varphi+2\pi k)/(8)), k=0,\ 1,\dots,7\}.](https://img.qammunity.org/2020/formulas/mathematics/high-school/8y6jpowyevycb2ddf1hxbcwdee7poivbej.png)
Now
at k=0,
![z_0=\sqrt[8]{1} (\cos(0+2\pi \cdot 0)/(8)+i\sin (0+2\pi \cdot 0)/(8))=1\cdot (1+0\cdot i)=1;](https://img.qammunity.org/2020/formulas/mathematics/high-school/j72ng0dtb2943jhrpi9htdd3r4m0b7gksl.png)
at k=1,
![z_1=\sqrt[8]{1} (\cos(0+2\pi \cdot 1)/(8)+i\sin (0+2\pi \cdot 1)/(8))=1\cdot ((√(2))/(2)+i(√(2))/(2))=(√(2))/(2)+i(√(2))/(2);](https://img.qammunity.org/2020/formulas/mathematics/high-school/se8wauuflo3s4s5bks2d7uq6pfuxm0aft1.png)
at k=2,
![z_2=\sqrt[8]{1} (\cos(0+2\pi \cdot 2)/(8)+i\sin (0+2\pi \cdot 2)/(8))=1\cdot (0+1\cdot i)=i;](https://img.qammunity.org/2020/formulas/mathematics/high-school/m5rwkmi92135camk89s9749hyutyfgcfx1.png)
at k=3,
![z_3=\sqrt[8]{1} (\cos(0+2\pi \cdot 3)/(8)+i\sin (0+2\pi \cdot 3)/(8))=1\cdot (-(√(2))/(2)+i(√(2))/(2))=-(√(2))/(2)+i(√(2))/(2);](https://img.qammunity.org/2020/formulas/mathematics/high-school/jl5dznsfw1zi21or0hmneafklbkkyk5gjb.png)
at k=4,
![z_4=\sqrt[8]{1} (\cos(0+2\pi \cdot 4)/(8)+i\sin (0+2\pi \cdot 4)/(8))=1\cdot (-1+0\cdot i)=-1;](https://img.qammunity.org/2020/formulas/mathematics/high-school/jzxbhlpyr4v0kgtk87b692555mocy7r2gb.png)
at k=5,
![z_5=\sqrt[8]{1} (\cos(0+2\pi \cdot 5)/(8)+i\sin (0+2\pi \cdot 5)/(8))=1\cdot (-(√(2))/(2)-i(√(2))/(2))=-(√(2))/(2)-i(√(2))/(2);](https://img.qammunity.org/2020/formulas/mathematics/high-school/3zid9j0alesrs3ilxvpl0ejnvj2selyu7y.png)
at k=6,
![z_6=\sqrt[8]{1} (\cos(0+2\pi \cdot 6)/(8)+i\sin (0+2\pi \cdot 6)/(8))=1\cdot (0-1\cdot i)=-i;](https://img.qammunity.org/2020/formulas/mathematics/high-school/kzvp9c1j2wpene6octgc0rczlmrdpmqyjy.png)
at k=7,
![z_7=\sqrt[8]{1} (\cos(0+2\pi \cdot 7)/(8)+i\sin (0+2\pi \cdot 7)/(8))=1\cdot ((√(2))/(2)-i(√(2))/(2))=(√(2))/(2)-i(√(2))/(2);](https://img.qammunity.org/2020/formulas/mathematics/high-school/ngcodnqw7lbopaznseq4afrwbjt994o6a4.png)
The 8th roots are
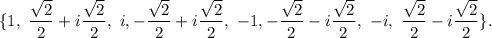
Option C is icncorrect.