Question

What is the total surface area of the code?

A) 273 cm2
B) 224 cm2
C) 147 cm2
D) 175 cm2

Answer 1

S.A = 704 cm^2

Explanation:

We know that the formula to find the surface area of a cone:

S.A =
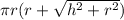`\pi r (r + √(h^2 + r^2) )`, where "r" is the radius and "h" is the height.

Given: r = 7 cm and h = 24 cm. The value of π = 22/7

Now plug in the given values in the above formula, we get

S.A =
`= (22)/(7) *7 (7 + \sqrt{24^(2)+ 7^2 } )`

S.A =
`22(7 + √(576 + 49) )`

S.A =
`22(7 + √(625) )`

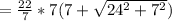
S.A = 22( 7 + 25)

S.A = 22(32)

S.A = 704 cm^2

The surface area of the cone is S.A = 704 cm^2.

Answer 2

Hello!

The answer is: None of the options.

The correct answer is:
`703.69cm^(2)`

Why?

The total surface area of the cone is equal to:

`TotalArea=BaseArea+LateralArea`

Calculations:

tex]BaseArea=\pi*r^{2}=\pi*7^{2}=153.94cm^{2}[/tex]

`LateralArea=BasePerimeter*SlantHeight/2\\BasePerimeter=2*\pi*r=2*\pi*7=43.98cm\\SlantHeight=\sqrt{height^(2)+radius^(2)  }=√(576+49)=√(625)=25`

[
`LateralArea=43.98*(25)/(2)=549.75cm^(2)`

So,

`TotalArea=153.94cm^(2) +549.75cm^(2)=703.69cm^(2)`

Have a nice day!