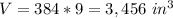Question

CAN SOMEONE PLEASE HELP ME SOLVE THIS!!

An architect is planning to make two triangular prisms out of iron. The architect will use ∆PQR for the bases of one prism and ∆XYZ for the bases of the other prism.

(A)What is the scale factor from ∆PQR to ∆XYZ?

(B) Suppose the height of the prism made by ∆PQR is 15 inches. What is the volume of the prism made by ∆PQR? Remember to show your work.

(C) Suppose the volume of the prism made by ∆PQR is 7776 〖"in" 〗^3. What is the volume of the prism made by ∆XYZ? Remember to show your work.

Answer 1

Part A) The scale factor is
`(2)/(3)`

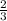
Part B)The volume of the prism made by ∆PQR is
`12,960\ in^(3)`

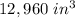
Part C) The volume of the prism made by ∆XYZ is
`3,456\ in^(3)`

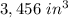
Explanation:

we know that

If two figures are similar, then the ratio of its corresponding sides is equal and this ratio is called the scale factor

In this problem triangles PQR and XYZ are similar

because

`(48)/(32)=(36)/(24)`

`48*24=32*36\\1,152=1,152`

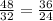
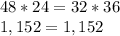
Part A) What is the scale factor from ∆PQR to ∆XYZ?

The scale factor is equal to
`(XY)/(PQ)=(32)/(48)=(2)/(3)`

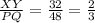
The scale factor is less than 1

therefore

Is a reduction

Part B) Suppose the height of the prism made by ∆PQR is 15 inches. What is the volume of the prism made by ∆PQR?

we know that

The volume of the triangular prism is equal to

`V=Bh`

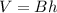
where

B is the area of the base of the prism ( area of triangle ∆PQR)

h is the height of the prism

Find the area of the base B

`B=(1)/(2)(36)(48)=864\ in^(2)`

`h=15\ in`

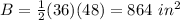
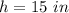
substitute the values

`V=864*15=12,960\ in^(3)`

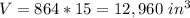
Part C) Suppose the volume of the prism made by ∆PQR is 7776 〖"in" 〗^3. What is the volume of the prism made by ∆XYZ?

step 1

Find the height of the prism made by ∆PQR

The volume of the triangular prism is equal to

`V=Bh`

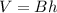
solve for h

`h=V/B`

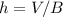
we have

`V=7,776\ in^(3)`

`B=864\ in^(2)`

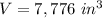
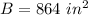
substitute in the formula

`h=7,776/864=9\ in`

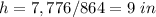
step 2

Find the volume of the prism made by ∆XYZ

The volume of the triangular prism is equal to

`V=Bh`

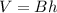
Find the area of the base B ∆XYZ

`B=(1)/(2)(24)(32)=384\ in^(2)`

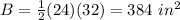
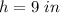`h=9\ in` -------> see step 1

substitute the values

`V=384*9=3,456\ in^(3)`