Question

A boat travels 26 miles East from a lighthouse then changes direction traveling 15(deg) South of West for 13 miles. How far is the ship from the lighthouse? Round to the nearest hundredth

Answer 1

Answer: 13.86

Explanation:

26^2 + 13^2 - (2)(26)(13)cos15°

= 192.03414142

√192.03414142

13.86 miles

Answer 2

The ship is 25.54 miles far from the light house.

Explanation:

It is given that A boat travels 26 miles East from a lighthouse then changes direction traveling 15° South of West for 13 miles that is :

BC=c, BA=26 miles and CA=13miles

Then, applying the cosine formula in ΔABC, we get

`(BC)^2=(BA)^2+(AC)^2-2(BA)(AC)cos15^(\circ)`

⇒
`c^2=(26)^2+(13)^2-2(26)(13)(0.965)`

⇒
`c^2=676+169-675(0.965)`

⇒
`c^2=652.34`

⇒
`c=25.54miles`

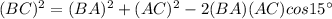
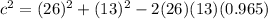
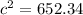
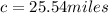
Therefore, the ship is 25.54 miles far from the light house.