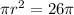Answer:
26pi
Explanation:
We are given a region satisfied by the equation as
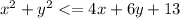
Rewrite this on left side and use completion of squares method
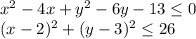
Thus the region is the interior of a cricle with centre at (2,3) and radius = square root of 26
Hence area = area of a circle
=