Question

A certain genetic condition affects 8% of the population in a city of 10,000. Suppose there is a test for the condition that has an error rate of 1% (i.e., 1% false negatives and 1% false positives).

Consider the values that would complete the table below.

Has condition Does not have condition totals

Test positive

Test negative

Totals

What is the probability (as a percentage) that a person has the condition if he or she tests positive? (Round your answer to one decimal place.)

Answer 1

Population in the city= 10,000

As genetic condition affects 8% of the population.

8 % of 10,000

`=(8)/(100)* 10,000=800`

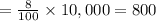
As, it is also given that, there is an error rate of 1% for condition (i.e., 1% false negatives and 1% false positives).

So, 1% false negatives means out of 800 tested who are found affected , means there are chances that 1% who was found affected are not affected at all.

So, 1% of 800
`=(1)/(100)* 800=8`

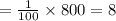
Also, 1% false positives means out of 10,000 tested,[10,000-800= 9200] who are found not affected , means there are chances that 1% who was found not affected can be affected also.

So, 1% of 9200
`=(1)/(100)* 9200=92`

1. Has condition Does not have condition totals = 800

2. Test positive =92

3. Test negative =8

4. Total =800 +92 +8=900

5. Probability (as a percentage) that a person has the condition if he or she tests positive= As 8% are found positive among 10,000 means 9200 are not found affected.But there are chances that out of 9200 , 1% may be affected

`=\frac{\text{1 percent of 9200}}{9200}\\\\ ((1)/(100)* 9200)/(9200)=(92)/(9200)\\\\ =0.01`

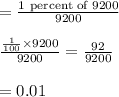
that is Probability equal to 0.01 or 1%.