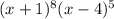Question

Find the least common multiple for 6(x+1)^3(x-4)^2 and 10(x+1)^8(x-4)^5

Answer 1

30
`(x+1)^8 (x-4)^5`

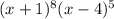
Explanation

`6(x+1)^(3)(x-4))^(2)=2X3 X (x+1)^3(x-4)^2\\10(x+1)^8(x-4)^5)= 2X5X(x+1)^8 (x-4)^5\\`

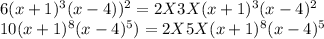
In order to find the Least common multiple we write each of the factor only once from each of the expression and for the common expression we take their LCM as maximum of the exponent in all expressions

as here in the question exponent of (x+1) are 3 and 8 so we take exponent 8

likewise for (x-4) we shall take maximum of 2 and 5 which is 5

so our expression for Least common multiple will be

2X3X5 X
`(x+1)^8 (x-4)^5`

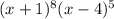
30
`(x+1)^8 (x-4)^5`