Given A(-12,5) and B(12,29) find the point that divides the line segment AB three-eighths of the way from A to B

Question

asked Aug 5, 2020 208k views

1 Answer

EliadL · Answer 1 · 2020-08-08T19:28:57+0000

Answer:

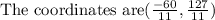
$\text{The coordinates are}((-60)/(11),(127)/(11))$

Explanation:

Given two points A(-12,5) and B(12,29). We have to find the point that divides the line segment AB three-eighths of the way from A to B.

By section formula, when a point C divides a segment AB in the ratio m:n, then the coordinates of point C are

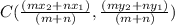
C(((mx_2+nx_1))/((m+n)),((my_2+ny_1))/((m+n)))

⇒
C(((3(12)+8(-12)))/((3+8)),((3(29)+8(5)))/((3+8)))

⇒
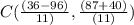
C(((36-96))/(11)),((87+40))/((11)))

⇒
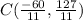
C((-60)/(11),(127)/(11))

Hence, the coordinates of point C that divides the line segment AB three eighths of the way from A to B are
((-60)/(11),(127)/(11))