Answer:
Explanation:
We are given the coordinates of a quadrilateral that is G(1,-1), H(5,1), I(4,3) and J(0,1).
Now, before proving that this quadrilateral is a rectangle, we will prove that it is a parallelogram. For this, we will prove that the mid points of the diagonals of the quadrilateral are equal, thus
Join JH and GI such that they form the diagonals of the quadrilateral.Now,
JH=
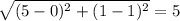 and
and
GI=
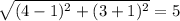
Now, mid point of JH=
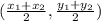
=
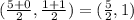
Mid point of GI=
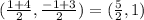
Since, mid point point of JH and GI are equal, thus GHIJ is a parallelogram.
Now, to prove that it is a rectangle, it is sufficient to prove that it has a right angle by using the Pythagoras theorem.
Thus, From ΔGIJ, we have
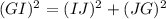 (1)
(1)
Now, JI=
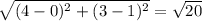 and GJ=
and GJ=
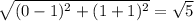
Substituting these values in (1), we get
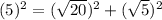
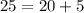
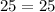
Thus, GIJ is a right angles triangle.
Hence, GHIJ is a rectangle.
Hence proved.