Question

Let f(x)=241+3e−1.3x . What is the point of maximum growth rate for the logistic function f(x) ? Round your answer to the nearest hundredth.

Answer 1

The yellow answer is the correct one

Explanation:

Answer 2

The point of maximum growth is at x=0.82

Explanation:

Given a logistic function

`f(x)=(24)/(1+e^(-1.3x))`

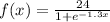
we have to find the point of maximum growth rate for the logistic function f(x).

From the graph we can see that the carrying capacity or the maximum value of logistic function f(x) is 24 and the point of maximum growth is at
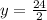`y=(24)/(2)` i.e between 0 to 12

So, we can take
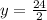`y=(24)/(2)` and then solve for x.

`(24)/(2)=(24)/(1+e^(-1.3x))`

⇒
`2=1+3exp(-1.3x)`

⇒
`1=3.exp(-1.3x)` ⇒
`(1)/(3)=exp(-1.3x)`

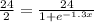
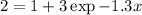
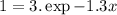⇒ log 3=-1.3x

⇒ -0.4771=-1.3.x ⇒ x=0.82

Hence, the point of maximum growth is at x=0.82