Question

Consider the following division of polynomials.

A) Use long division to determine the quotient of the polynomials. Show all of your work for full credit.
B) Use mathematical methods to prove your answer. Show all of your work for full credit.

Answer 1

`x^4=x^2\cdot x^2`. Multiplying the denominator by
`x^2` gives

`x^2(x^2+2x+8)=x^4+2x^3+8x^2`

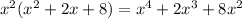
Subtracting this from the numerator gives a remainder of

`(x^4+x^3+7x^2-6x+8)-(x^4+2x^3+8x^2)=-x^3-x^2-6x+8`

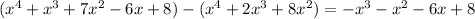
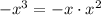`-x^3=-x\cdot x^2`. Multiplying the denominator by
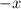`-x` gives

`-x(x^2+2x+8)=-x^3-2x^2-8x`

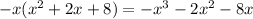
and subtracting this from the previous remainder gives a new remainder of

`(-x^3-x^2-6x+8)-(-x^3-2x^2-8x)=x^2+2x+8`

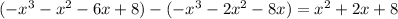
This last remainder is exactly the same as the denominator, so
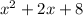`x^2+2x+8` divides through it exactly and leaves us with 1.

What we showed here is that

`(x^4+x^3+7x^2-6x+8)/(x^2+2x+8)=x^2-(x^3+x^2+6x-8)/(x^2+2x+8)`

`=x^2-x+(x^2+2x+8)/(x^2+2x+8)`

`=x^2-x+1`

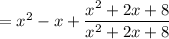
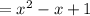
and this last expression is the quotient.

To verify this solution, we can simply multiply this by the original denominator:

`(x^2+2x+8)(x^2-x+1)=x^2(x^2-x+1)+2x(x^2-x+1)+8(x^2-x+1)`

`=(x^4-x^3+x^2)+(2x^3-2x^2+2x)+(8x^2-8x+8)`

`=x^4+x^3+7x^2-6x+8`

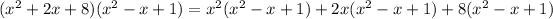
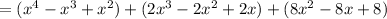
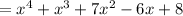
which matches the original numerator.

Answer 2

Explanation:

A) Long division :

x²+2x+8) x⁴+ x³+ 7x²-6x+8 ( x²-x+1

x⁴+2x³+8x²

-x³ -x² -6x

-x³ -x² -8x

x² +2x + 8

x² +2x + 8

NIL

B) By multiplying (x² + 2x + 8) and quotient (x²-x+1) We should get the expression (x⁴+x³+7x²-6x+8) as of numerator.

(x²+2x+8) × (x²-x+1)

= x²(x²-x+1) + 2x(x²-x+1)+8(x²-x+1)

= x⁴-x³+x²+2x³-2x²+2x+8x²-8x+8

= (x⁴+x³+7x²-6x+8)

Hence proved.