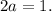Question

Find the constant difference for a hyperbola with foci (-3.5, 0) and (3.5, 0) and a point on the hyperbola (3. 5, 24).

Answer 1

2a=1

Explanation:

The constant difference for a hyperbola
`(x^2)/(a^2)-(y^2)/(b^2)=1` is
`2a.`

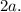
1. Since hyperbola has foci (-3.5, 0) and (3.5, 0), then
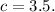`c=3.5.` Note that
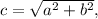`c=√(a^2+b^2),` then

`√(a^2+b^2)=3.5\Rightarrow a^2+b^2=3.5^2.`

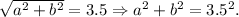
2. Since point (3.5,24) lies on the hyperbola, then

`(3.5^2)/(a^2)-(24^2)/(b^2)=1.`

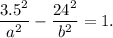
3. Solve the system of two equations:

`\left\{\begin{array}{l}a^2+b^2=3.5^2\\(3.5^2)/(a^2)-(24^2)/(b^2)=1\end{array}\right.`

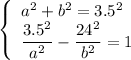
From the 1st equation,

`b^2=3.5^2-a^2,`

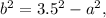
then

`(3.5^2)/(a^2)-(24^2)/(3.5^2-a^2)=1,\\ \\(3.5^2(3.5^2-a^2)-24^2a^2)/(a^2(3.5^2-a^2))=1,\\ \\3.5^4-3.5^2a^2-24^2a^2=3.5^2a^2-a^4,\\ \\a^4-a^2(2\cdot 3.5^2+24^2)+3.5^4=0,\\ \\a^4-600.5a^2+150.0625=0,\\ \\D=(-600.5)^2-4\cdot 150.0625=360000,\\ \\a^2_(1,2)=(600.5\pm 600)/(2)=(1)/(4),600(1)/(4).`

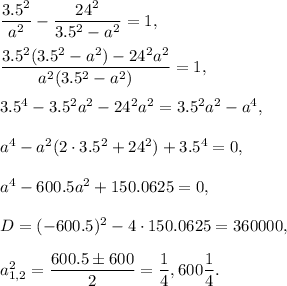
For
`a^2=(1)/(4),\ b^2=3.5^2-0.25=12.`

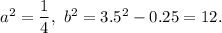
For
`a^2=600(1)/(4),\ b^2=3.5^2-600.25<0,` this is impossible, then
`a^2=600(1)/(4)` is extra solution.

Hence,
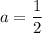`a=(1)/(2)` and
`2a=1.`