Answer:
The value remains under the radical is 8.
Explanation:
Given : When 1250 to the 3/4 power is written in simplest radical form.
To find : Which value remains under the radical?
Solution :
The expression is written as
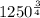
Applying property,
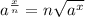
So,
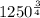
![=\sqrt[4]{1250^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/srr9n2arp9e92rnz35gpexdopq3eqevtzz.png)
![=\sqrt[4]{1250* 1250* 1250}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/5rqgucl7gd0hv4yons43mz60nid8if6htj.png)
![=\sqrt[4]{5^4(2)* 5^4(2)* 5^4(2)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/j7084oau20clowgp7byodjfq22ga4veqja.png)
![=5* 5* 5\sqrt[4]{2^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/fsldjkbver1uag2hwdjdgie6ak92mpiv1b.png)
![=125\sqrt[4]{8}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jla2ykk8gol5hcsdz6dv301tj36sqwhsme.png)
Therefore, The value remains under the radical is 8.