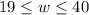Answer:
We can write the range for w as :
Explanation:
The perimeter of rectangle is given as :
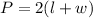 or
or
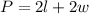
Where l = length and w = width
Given is : the length of the garden is 16 feet
Also given is that the perimeter of the garden must be at least 70 feet and no more than 112 feet.
So, this can be shown as :
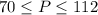
=>
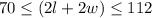
Putting l = 16
=>
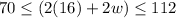
=>
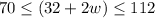
=>
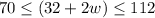
=>
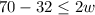 and
and
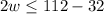
=>
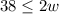 and
and

=>
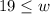 and
and
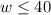
So, we can write the range for w as :