Subdividing [0, 1] into 10 equally spaced intervals of length
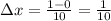 gives the partition
gives the partition
![[0,1] = \left[0,\frac1{10}\right] \cup \left[\frac1{10},\frac2{10}\right] \cup \cdots \cup \left[\frac9{10},1\right]](https://img.qammunity.org/2023/formulas/advanced-placement-ap/college/1j0nbdyrbyrpdost2htu0zcge49x2natn3.png)
The
 -th subinterval has left and right endpoints, respectively, given by
-th subinterval has left and right endpoints, respectively, given by
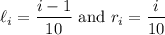
where
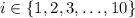 .
.
The midpoint of the
 -th interval is the average of these,
-th interval is the average of these,
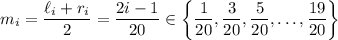
We approximate the area under
 over [0, 1] by the Riemann sum,
over [0, 1] by the Riemann sum,
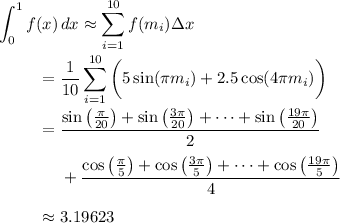
(D)