Answer:
The simplified value of given expression is 1, which is free from a, therefore the value of the expression does not depend on the variable a.
Explanation:
The given expression is
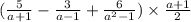
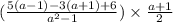
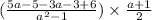
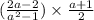
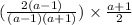
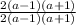
Cancel out the common factors.
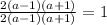
Since the simplified value of given expression is 1, which is free from a, therefore the value of the expression does not depend on the variable a.