2)
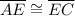 (a segment bisector splits a segment into two congruent parts)
(a segment bisector splits a segment into two congruent parts)
3)
 (a segment bisector splits a segment into two congruent parts)
(a segment bisector splits a segment into two congruent parts)
4)
 (vertical angles are congruent)
(vertical angles are congruent)
5)
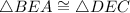 (SAS)
(SAS)
6)
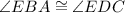 (CPCTC)
(CPCTC)
7)
 (converse of alternate interior angles theorem)
(converse of alternate interior angles theorem)
8)
 (vertical angles are congruent)
(vertical angles are congruent)
9)
 (SAS)
(SAS)
10)
 (CPCTC)
(CPCTC)
11)
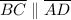 (converse of alternate interior angles theorem)
(converse of alternate interior angles theorem)