Is the system of equations is consistent, consistent and coincident, or inconsistent? y=4x−4y=−4x+4 Select the correct answer from the drop-down menu.

Question

asked Nov 22, 2020 153k views

2 Answers

Evan Hobbs · Answer 1 · 2020-11-23T12:31:41+0000

Answer:

The given system of equations is consistent.

Explanation:

The given equations are

y=4x-4 (1)

y=-4x+4 (2)

Add both equations,

2y=0

y=0

Put this value in 1.

0=4x-4

x=1

Using the elimination method the solution of given equations is (1,0).

Since the system of equations has a solution, therefore the given system of equations is consistent.

Hetzroni · Answer 2 · 2020-11-29T03:18:16+0000

Answer: It is consistent as the lines are intersecting lines and it has a unique solution

Explanation:

Since we have given two systems of equation :

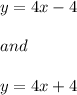
$y=4x-4\\\\and\\\\y=4x+4$

We need to check whether the system of equations is consistent or inconsistent.

As we know the formula for checking the consistency :

(a_1)/(a_2)=(b_1)/(b_2)=(c_1)/(c_2)

In first equation we have

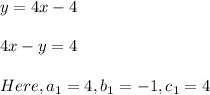
$y=4x-4\\\\4x-y=4\\\\Here,a_1=4,b_1=-1,c_1=4$

similarly,

In the second equation we have

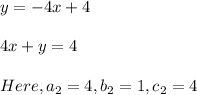
$y=-4x+4\\\\4x+y=4\\\\Here,a_2=4,b_2=1,c_2=4$

So, According to question, we have

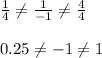
$(1)/(4)\\eq (1)/(-1)\\eq (4)/(4)\\\\0.25\\eq -1\\eq 1$

Hence, it is consistent as the lines are intersecting lines and it has a unique solution.