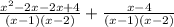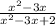Question

Anyone know how to do this

Answer 1

\frac{x^2-3x}{x^2-3x+2}

Explanation:

We are given the following rational expressions and we are to add them:

`\frac {x^2 + x-6 } {x^2 + 2x-3 } + \frac {x - 4} {x^2 - 3 x + 2}`

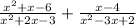
To solve this, first of all we will factorize the quadratic expression in the numerator and the denominator to make it easy and then cancel out the like terms to simplify it.

`\frac {x^2 + 3x - 2x - 6} {x^2 + 3x - 1x - 3} + \frac {x - 4} {x^2 - 2x - x + 2}`

`(x(x+3)-2(x+3))/(x(x+3)-1(x+3)) +(x-4)/(x(x-1)-2(x-1))`

`((x+3)(x-2))/((x+3)(x-1)) +((x-4))/((x-1)(x-2))`

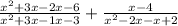
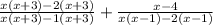
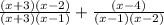
Cancelling out the like terms, we get:

`(x-2)/(x-1) +(x-4)/((x-2)(x-1))`

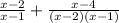
Taking LCM and combing the terms to get:

`(x^2-2x-2x+4)/((x-1)(x-2)) +(x-4)/((x-1)(x-2))`

`(x^2-3x)/(x^2-3x+2)`

Answer 2

Final answer is
`(x^2-3x)/(x^2-3x+2)`

Explanation:

`(x^2+x-6)/(x^2+2x-3)+(x-4)/(x^2-3x+2)`

In this type of problems, we factor numerator and denominator whichever possible. then make denominators equal and combine numerator.

Then simplify to get the answer.
`=(x^2+x-6)/(x^2+2x-3)+(x-4)/(x^2-3x+2)`

`=(x^2+3x-2x-6)/(x^2+3x-1x-3)+(x-4)/(x^2-1x-2x+2)`

`=(x\left(x+3\right)-2\left(x+3\right))/(x\left(x+3\right)-1\left(x+3\right))+(x-4)/(x\left(x-1\right)-2\left(x-1\right))`

`=(\left(x-2\right)\left(x+3\right))/(\left(x-1\right)\left(x+3\right))+(x-4)/(\left(x-2\right)\left(x-1\right))`

`=(\left(x-2\right))/(\left(x-1\right))+(x-4)/(\left(x-2\right)\left(x-1\right))`

`=(\left(x-2\right))/(\left(x-1\right))\cdot(\left(x-2\right))/(\left(x-2\right))+(x-4)/(\left(x-2\right)\left(x-1\right))`

`=(x^2-2x-2x+4)/(\left(x-1\right)\left(x-2\right))+(x-4)/(\left(x-2\right)\left(x-1\right))`

`=(x^2-2x-2x+4+x-4)/(\left(x-1\right)\left(x-2\right))`

`=(x^2-3x)/(x^2-2x-1x+2)`

`=(x^2-3x)/(x^2-3x+2)`

Hence final answer is
`(x^2-3x)/(x^2-3x+2)`