Answer:
The length of the pendulum is 8 units
Explanation:
The period T (in seconds) of a pendulum is given by
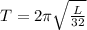 .
.
We want to find the value of
 , when
, when
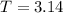 and
and
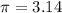 .
.
We substitute the given values into the formula to get,
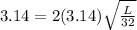 .
.
We divide through by 3.14 to get,
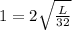 .
.
We divide both sides by 2, to obtain,
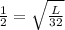 .
.
We square both sides to get,
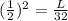

We now multiply both sides by 32 to get,
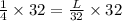
We cancel out the common factors to get,

Hence,the length of the pendulum is 8 units