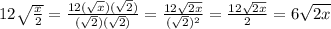Question

Which is equivalent to 4 square root of 9 1/2x?

Answer 1

B. 9 ^ 1/8x

Explanation:

just did it and got it right

Answer 2

Answer:
`6√(2x)`

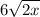
Explanation:

1. You have the following expression given in the problem above:

`4\sqrt{(9x)/(2) }`

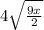
2. Remove the perfects squares from the square root:

`9=3^(2)`

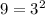
Then:

`4*3\sqrt{(x)/(2)}=12\sqrt{(x)/(2)}`

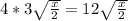
3. Now, rationalize the denominator, because it cotains an square root. Multiply the numerator and the denominator by
`√(2)` and simplify, as following:

`12\sqrt{(x)/(2)}=(12(√(x))(√(2)))/((√(2))(√(2)))=(12√(2x))/((√(2))^(2))=(12√(2x))/(2)=6√(2x)`