Answer:
C. 180
Explanation:
We are given that the arithmetic series consists of integers that are multiples of 4 with first term 0.
So,we get the series as,
0, 4, 8, 12, 16, 20, 24, 28, 32, 36.
Now, it is required to find the sum of first nine non-zero terms.
We have the sum of the arithmetic series is given by,
![S_(n)=(n)/(2) * [2a+(n-1)d]](https://img.qammunity.org/2020/formulas/mathematics/high-school/xxwhcdp4gdwi5cz8ikb9ia4ak03hmg93ef.png)
where a = 4 and d = 8-4 = 4.
Substituting the values, we get,
![S_(n)=(n)/(2) * [2 * 4+4(n-1)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/uqbflg7smtf5og0v2udfblxoo8wafwvx1l.png)
As, we want the sum of first nine non-zero terms, this gives n=9
So,
![S_(9)=(9)/(2) * [2 * 4+4(9-1)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/aluhgo71q0onttp49clmzux6k92pad7jqr.png)
i.e.
![S_(9)=(9)/(2) * [2 * 4+4 * 8]](https://img.qammunity.org/2020/formulas/mathematics/high-school/w784w3ppmokgj8cx01tn0qux0swfe7abcd.png)
i.e.
![S_(9)=(9)/(2) * [8+32]](https://img.qammunity.org/2020/formulas/mathematics/high-school/8bsgocop4iwi6eh7c5tzlyqnacx2lxkl5o.png)
i.e.
![S_(9)=(9)/(2) * [40]](https://img.qammunity.org/2020/formulas/mathematics/high-school/l8hvh6gadb3geacied0pj5c28oepx6aoqt.png)
i.e.
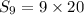
i.e.
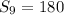
Hence, the sum of first nine non-zero terms is 180.