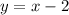Question

What is the equation of the oblique asymptote.

h(x)=x^2-x-2/x+1


A.) y=x

B.) y=x-2

C.) y=x^2+1

D.) y=x+1

Answer 1

The asymptote of a curve is a straight line, to which curve in the case of distance to infinity approaches arbitrarily close.

If the curve given by the equation y = f (x) is reduced to infinity when x approaches a finite point a, then the line x = a is called the vertical asymptote of this curve.

x =
`(x^(2) -x-2)/(x+1)`

x =
`(x^(2)-x-2 )/(x+1)`, x≠-1

x =
`(x^(2) +x-2x -2)/(x+1)`

x =
`(x*(x+1) - 2 (x+1))/(x+1)`

x =
`((x+1) * (x-2))/(x+1)`

x = x -2

0 = -2

x ∈ ∅

Answer 2

Option: B is the correct answer.

B.
`y=x-2`

Explanation:

The oblique asymptote occur when the degree of the numerator term is greater than the degree of the denominator term.

It is also known as the slant asymptote.

In order to find this we divide the numerator term by the denominator term and hence the resultant i.e. the quotient is the oblique asymptote.

Here we have a rational function as:

`h(x)=(x^2-x-2)/(x+1)\\\\\\i.e.\\\\h(x)=(x^2-2x+x-2)/(x+1)\\\\i.e.\\\\h(x)=(x(x-2)+1(x-2))/(x+1)\\\\i.e.\\\\h(x)=((x+1)(x-2))/(x+1)\\\\i.e.\\\\h(x)=x-2`

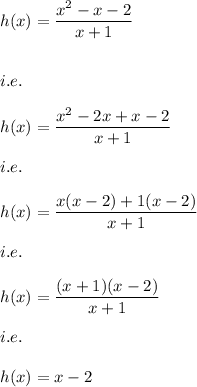
Hence, the oblique asymptote is:

`y=x-2`