Answer:
8 cm
Explanation:
Consider trapezoid ABCD with bases AB and DC. In these trapezoid triangles AOB and COD are similar, because thet have three pairs of congruent angles (angles AOB and COD are congruent as vertical angles, angles OAB and OCD are congruent as corresponding angles and angles OBA and ODC are congruent as corresponding angles too). Then
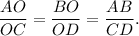
If
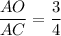 and
and
 then
then
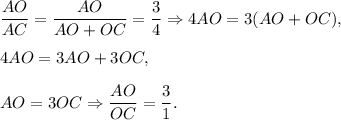
Since BO=6 cm, then
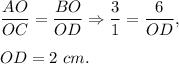
Thus, the length of the diagonal BD is 2+6=8 cm.