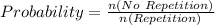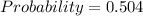Question

A typical ID number in a college class consists of a four-digit number, such as 0119. When an ID number is randomly selected, what is the probability that no two of its digits are the same

Answer 1

`Probability = 0.504`

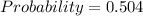
Explanation:

Given

`ID: 4\ digit\ number`

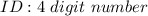
Required

Determine the probability that no two digit is repeated

First, we need to determine the total possible number of pins (with repetition)

Each of the 4 ID digit can be selected from any of the 10 digits (0 - 9).

i.e.

`First = 10`

`Second = 10`

`Third = 10`

`Fourth = 10`

`Total = 10 * 10 * 10 * 10`

`Total = 10000`

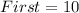
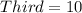
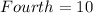
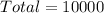
i.e.

`n(Repetition) = 10000`

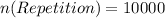
Next, we determine the total possible number of pins (without repetition)

Once a digit is selected from any of the 10 digits (0 - 9), it can no longer be repeated.

i.e.

`First = 10`

`Second = 10 - 1 = 9`

`Third = 10 - 1 - 1= 8`

`Fourth = 10 - 1 - 1 - 1 = 7`

`Total = 10 * 9 * 8 * 7`

`Total = 5040`

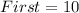
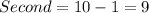
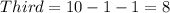
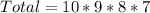
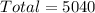
i.e.

`n(No\ Repetition) = 5040`

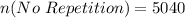
The probability is then calculated as:

`Probability = (n(No\ Repetition))/(n(Repetition))`

`Probability = (5040)/(10000)`

`Probability = 0.504`