Question

Solve with cramer's rule x+2y+3z=11, 2x+y+2z=10, 3x+2y+z=9

Answer 1

x = 2 , y = 0 , z = 3

Explanation:

Cramer's rule is a rule through which we can find the solution of linear equation.

we have the three linear equations as

x+2y+3z=11

2x+y+2z=10

3x+2y+z=9

AX=B

A: coefficient matrix

X= unknown vectors(x,y,z)

D = values of the linear equation (11 , 10 , 9)

now we find the determinant of the given linear equation

determinant of the matrix will be

A =
`\left[\begin{array}{ccc}1&2&3\\2&1&2\\3&2&1\end{array}\right]` = 1(1-4) - 2(2-6) + 3(4 - 3)

= 1(-3) - 2(-4) + 3(1)

= -3+8+3 = 8

also D
`\\eq 0`

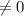
so the determinant is Non zero we can apply Cramer's rule

we will be replacing the first column of the coefficient matrix A with the values of D

by replacing the first column we will get the value of the variable 'x'

Dx =
`\left[\begin{array}{ccc}11&2&3\\10&1&2\\9&2&1\end{array}\right]` = 11(1-4) -2(10-18) + 3(20-9) = -33+16+33 = 16

x =
`(Dx)/(D)` =
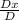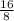`(16)/(8)` = 2

similarly

Dy =
`\left[\begin{array}{ccc}1&11&3\\2&10&2\\3&9&1\end{array}\right]` = 1(10-18) -11(2-6) + 3(18 -30) = -8 +44 -36 = 0

y =
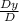`(Dy)/(D)` = 0

Dz=
`\left[\begin{array}{ccc}1&2&11\\2&1&10\\3&2&9\end{array}\right]` = 1(9 - 20) -2(18 - 30) + 11(4 -3) = -11 +24 +11 = 24

z =
`(Dz)/(D)` =
`(24)/(8) = 3`

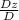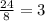
so we have the solution as

x = 2 , y = 0 , z = 3

Therefore the solution for the given linear equations is (2,0,3).