Answer:
The given parameters are;
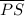 ≅
≅
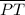 , ∠PRS ≅ ∠PRT
, ∠PRS ≅ ∠PRT
To prove that ΔPRS ≅ ΔPRT
A two column proof is given as follows;
Statement
 Reason
Reason
∠PRS and ∠PRT are ≅
 Given
Given
∠PRS and ∠PRT are
 ∡ that form a linear pair are supplementary
∡ that form a linear pair are supplementary
supplementary angles
∠PRS and ∠PRT are right ∡
 Two ≅ and supplementary angles are right ∡
Two ≅ and supplementary angles are right ∡
ΔPRS and ΔPRT are right Δ
 Triangle with one angle = 90°
Triangle with one angle = 90°
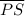 ≅
≅

 Given
Given
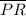 ≅
≅
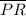
 Reflective property
Reflective property
ΔPRS ≅ ΔPRT
 By hypotenuse leg postulate.
By hypotenuse leg postulate.
Explanation:
The given parameters are;
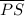 ≅
≅
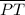 , ∠PRS ≅ ∠PRT
, ∠PRS ≅ ∠PRT
To prove that ΔPRS ≅ ΔPRT
A two column proof is given as follows;
Statement
 Reason
Reason
∠PRS and ∠PRT are congruent
 Given
Given
2) ∠PRS and ∠PRT are supplementary angles by angles that form a linear pair are supplementary
3) ∠PRS and ∠PRT are right angles by
 Two congruent angles which are also supplementary (sum up to 180°) are two 90° angles
Two congruent angles which are also supplementary (sum up to 180°) are two 90° angles
4) ΔPRS and ΔPRT are right triangles
 Triangle with one angle = 90°
Triangle with one angle = 90°
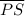 ≅
≅

 Given
Given
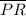 ≅
≅
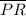
 Reflective property
Reflective property
ΔPRS ≅ ΔPRT
 By hypotenuse leg postulate for the congruency of two right triangles.
By hypotenuse leg postulate for the congruency of two right triangles.