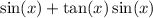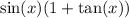Question

Simplify the following expression to its simplest form

Answer 1

Explanation:

`\sin(\pi - x) + \tan(x) \cos(x) (x - (\pi)/(2)`

`\sin( - x + \pi ) + \tan(x) ( \cos(x - (\pi)/(2) ) )`

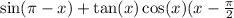
Sin is odd function, so if you add pi to it, it would become switch it sign.

`- \sin( - x) + \tan(x) \cos(x - (\pi)/(2) )`

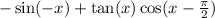
Also since sin is again, a odd function, we can just multiply the inside and outside by -1, and it would stay the same.

`\sin(x) + \tan(x) \cos(x - (\pi)/(2) )`

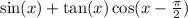
Cosine is basically a sine function translated pi/2 units to the right or left so

`\sin(x) + \tan(x) \sin(x)`

`\sin(x) ( 1 + \tan(x) )`