Solution :
To claim to be tested is whether "the mean salary is higher than 48,734".
i.e. μ > 48,734
Therefore the null and the alternative hypothesis are

and
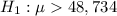
Here, n = 50
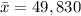
s = 3600
We take , α = 0.05
The test statistics t is given by
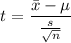

t = 2.15
Now the ">" sign in the
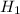 sign indicates that the right tailed test
sign indicates that the right tailed test
Now degree of freedom, df = n - 1
= 50 - 1
= 49
Therefore, the p value = 0.02
The observed p value is less than α = 0.05, therefore we reject
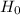 . Hence the mean salary that the accounting graduates are offered from the university is more than the average salary of 48,734 dollar.
. Hence the mean salary that the accounting graduates are offered from the university is more than the average salary of 48,734 dollar.