Given:
x, y and z are integers.
To prove:
If
 is even, then at least one of x, y or z is even.
is even, then at least one of x, y or z is even.
Solution:
We know that,
Product of two odd integers is always odd. ...(i)
Difference of two odd integers is always even. ...(ii)
Sum of an even integer and an odd integer is odd. ...(iii)
Let as assume x, y and z all are odd, then
 is even.
is even.
 is always odd. [Using (i)]
is always odd. [Using (i)]
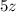 is always odd. [Using (i)]
is always odd. [Using (i)]
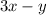 is always even. [Using (ii)]
is always even. [Using (ii)]
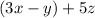 is always odd. [Using (iii)]
is always odd. [Using (iii)]
 is always odd.
is always odd.
So, out assumption is incorrect.
Thus, at least one of x, y or z is even.
Hence proved.