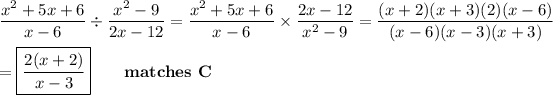Question

What is the answer? Really confused on how to figure this out

Answer 1

`C.(2(x+2))/((x-3))`

Explanation:

`(x^2+5x+6)/(x-6) / (x^2-9)/(2x-12) \\\\Now,\\Before\ touching\ the\ expression,\ lets\ look\ at\ the\ indiviual\ terms\ and\ try\ to factorize\ them.\\x^2+5x+6\\=(x^2+3x+2x+6)\\=x(x+3)+2(x+3)\\=(x+2)(x+3)\\\\x-6=(x-6)\\\\x^2-9\\=(x)^2-(3)^2\\=(x-3)(x+3)\\\\2x-12\\=2(x-6)\\\\Hence,\\(x^2+5x+6)/(x-6) / (x^2-9)/(2x-12)\\=((x+3)(x+2))/(x-6) / ((x-3)(x+3))/(2(x-6))\\By\ flipping\ the\ second\ term\ to\ its\ reciprocal, we\ get:\\`
`((x+3)(x+2))/(x-6) * (2(x-6))/((x-3)(x+3))\\\\=(x+2)*(2)/((x-3)) \\=(2(x+2))/((x-3))`

Answer 2

9514 1404 393

Answer:

C. 2(x+2)/(x-3)

Explanation:

As with division of any fractions, it works well to multiply by the inverse of the denominator. You simplify this by cancelling common factors from the resulting numerator and denominator.

To find the factors, you must factor each of the quadratics. Here, factors of (x+3) and (x-6) cancel.

`(x^2+5x+6)/(x-6)/(x^2-9)/(2x-12)=(x^2+5x+6)/(x-6)*(2x-12)/(x^2-9)=((x+2)(x+3)(2)(x-6))/((x-6)(x-3)(x+3))\\\\=\boxed{(2(x+2))/(x-3)}\qquad\textbf{matches C}`