Given:
Total number of calculators in a box = 10
Defective calculators in the box = 1
To find:
The number of ways in which four calculators be selected and one of the four calculator is defective.
Solution:
We have,
Total calculators = 10
Defective calculators = 1
Then, Non-defective calculator = 10-1 = 9
Out of 4 selected calculators 1 should be defective. So, 3 calculators are selected from 9 non-defective calculators and 1 is selected from the defective calculator.
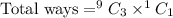
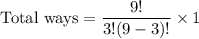
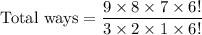

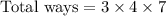

Therefore, the four calculators can be selected in 84 ways.